Friday, February 26, 2016
Verilog HDL: 1-bit Full Adder Gate-level Circuit Description
This is a gate-level description of a 1-bit Full Adder. We use 2 Half Adder modules to return the Sum and Carry out of the inputs.
Structural Diagram Full Adder Module
Half Adder Module
Full Adder Testbench
If you have any question, please, post a comment below.
Structural Diagram Full Adder Module
module FullAdder(A,B,Cin,Cout,S);
input A,B,Cin;
wire C1,C2,S1;
output Cout,S;
HalfAdder UUT1(.x(A), .y(B), .c(C1), .s(S1)); // S1 = (A)xor(B); C1 = (A)and(B);
HalfAdder UUT2(.x(Cin), .y(S1), .c(C2), .s(S)); // S = (Cin)xor(S1); C2 = (Cin)and(S1);
or G1(Cout,C1,C2); // Cout = (C1)or(C2);
endmodule
Half Adder Module
module HalfAdder(x,y,c,s);
input x,y;
output c,s;
xor G1(s,x,y); // s = (x) xor (y)
and G2(c,x,y); // c = (x) and (y);
endmodule
Full Adder Testbench
module tb_FullAdder;
reg A,B,Cin;
wire Cout,S;
FullAdder UUT(.A(A), .B(B), .Cin(Cin), .Cout(Cout), .S(S)); // Testing FullAdder Module
initial begin
$dumpfile("FullAdder.vpd");
$dumpvars;
A=0; B=0; Cin=0; #10 // Testing all possible values...
A=0; B=0; Cin=1; #10
A=0; B=1; Cin=0; #10
A=0; B=1; Cin=1; #10
A=1; B=0; Cin=0; #10
A=1; B=0; Cin=1; #10
A=1; B=1; Cin=0; #10
A=1; B=1; Cin=1; #10
$finish;
end
endmodule
If you have any question, please, post a comment below.
Sunday, January 10, 2016
Embedded Systems: Turn on LEDs with the push buttons of the MB90F387S MCU (Fujitsu Jouet Bleu Starter Kit)
Shinemax24
9:04 PM
Digital Systems Design
,
Embedded Systems
,
Fujitsu Jouet Bleu Starter Kit
,
MB90F387S MCU
No comments
:
In this program, we will make the integrated LEDs turn on and off upon the press of switches.
We will make LED1, LED3, and LED5 turn on when SW1 is pressed and make LED2, and LED3 turn on when SW2 is pressed. These LEDs turn off when the respective push buttons are released.
If you have any question, please, post a comment below.
We will make LED1, LED3, and LED5 turn on when SW1 is pressed and make LED2, and LED3 turn on when SW2 is pressed. These LEDs turn off when the respective push buttons are released.
#include "_ffmc16.h"
#include "extern.h"
#include "monitor.h"
void main(void)
{
__set_il(7);
__EI();
IO_PDR1.byte=0x1F; //Set LEDs 1-5 to off
IO_DDR1.byte=0x1F; //Configure LEDs 1-5 as output
IO_DDR2.byte=0x00; //Configure SW1 and SW2 as input
while(1) //while system is on
{
if(IO_PDR2.bit.P25==1) //If SW1 is not pressed
{
IO_PDR1.bit.P10=1; //Turn off LED1
IO_PDR1.bit.P12=1; //Turn off LED3
IO_PDR1.bit.P14=1; //Turn off LED5
}
else //If SW1 is pressed
{
IO_PDR1.bit.P10=0; //Turn on LED1
IO_PDR1.bit.P12=0; //Turn on LED3
IO_PDR1.bit.P14=0; //Turn on LED5
}
if(IO_PDR2.bit.P27==1) //If SW2 is not pressed
{
IO_PDR1.bit.P11=1; //Turn off LED2
IO_PDR1.bit.P13=1; //Turn off LED4
}
else //If SW2 is pressed
{
IO_PDR1.bit.P11=0; //Turn on LED2
IO_PDR1.bit.P13=0; //Turn on LED4
}
}
}
/**************************************************************************************************
Interrupt Routine
**************************************************************************************************/
__interrupt void reload_int(void)
{
}
__interupt void ADC_int(void)
{
}
__interrupt void ext_int(void)
{
}
#pragma section INTVECT, locate=0xfffc00
#pragma intvect _start 0x8 0x0
#pragma intvect reload_int 17
#pragma intvect ADC_int 18
#pragma intvect ext_int 24
If you have any question, please, post a comment below.
Thursday, March 5, 2015
Logic Circuits: 1-digit Decimal in Excess-3 to Gray Code Converter
Problem: Design a digital circuit that converts an Excess-3 of a single-digit decimal input into Gray Code. Draw it's logic diagram.
In order to be able to design this circuit ourselves, we need to learn Excess-3 and Gray Code. We can familiarize ourselves to them at least.
First step in designing the circuit is to generate it's Truth Table. Let's label the inputs as A, B, C, and D and outputs as W, X, Y, and Z.
Based from what we've learned, Decimal 0 in Excess-3 is 0011 and Decimal 9 is 1100. Therefore, we will not care about the other outputs, thus, labeling them as Don't-cares (X). Be careful with the output as the required output is Gray Code.
Second step is finding the boolean functions of each of the outputs. Let us use Karnaugh maps (K-map). Learn about K-map through these examples here.
Third step is to test the circuit manually by analysis, construction, or simulation of the circuit in some software. Here, let us simulate the circuit. If you have Proteus, download the Proteus 8 project file here (Dropbox link) for the circuit simulation.
Finally, we need to draw the logic diagram of our design since it is being required.
A, B, C, and D are the inputs. W, X, Y, and Z are the outputs. If you have any question, place a comment below.
In order to be able to design this circuit ourselves, we need to learn Excess-3 and Gray Code. We can familiarize ourselves to them at least.
First step in designing the circuit is to generate it's Truth Table. Let's label the inputs as A, B, C, and D and outputs as W, X, Y, and Z.
 |
| Single-digit Decimal in Excess-3 to Gray Code Converter Truth Table |
Second step is finding the boolean functions of each of the outputs. Let us use Karnaugh maps (K-map). Learn about K-map through these examples here.
 |
| W = AB + ACD |
 |
| X = A + BCD |
 |
| Y = B'C'D' + BD + BC |
 |
| Z = C' |
Third step is to test the circuit manually by analysis, construction, or simulation of the circuit in some software. Here, let us simulate the circuit. If you have Proteus, download the Proteus 8 project file here (Dropbox link) for the circuit simulation.
 |
| Simulation Screenshot |
Finally, we need to draw the logic diagram of our design since it is being required.
 |
| Logic Diagram of the circuit |
Monday, February 16, 2015
C Programming: Non-recursive and Recursive Programs for Getting the Factorial of a Number
Here are programs that compute for the factorial of a number both non-recursively and recursively.
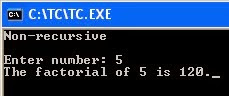
Here is the non-recursive way:
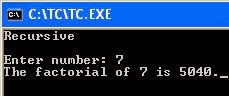
Here is the recursive way:
If you have questions on these, place a comment below.
Here is the non-recursive way:
#include<stdio.h>
int factorial(int num)
{
int i;
for(i=num-1;i>1;i--)
{
num=num*i;
}
return num;
}
main()
{
int num,ans;
clrscr();
printf("Non-recursive\n\n");
printf("Enter number: ");
scanf("%d",&num);
ans=factorial(num);
printf("The factorial of %d is %d.",num,ans);
getch();
}
Here is the recursive way:
#include<stdio.h>
int factorial(int num)
{
if(num==1) //We don't have to multiply the number by 1 since it will just be the same number
{
return 1;
}
else
{
num=num*factorial(num-1);
return num;
}
}
main()
{
int num,ans;
clrscr();
printf("Recursive\n\n");
printf("Enter number: ");
scanf("%d",&num);
ans=factorial(num);
printf("The factorial of %d is %d.",num,ans);
getch();
}
If you have questions on these, place a comment below.
Friday, February 6, 2015
C Programming: Stacking with a Singly Linked List of Nested Structures (2 Structures)
Shinemax24
8:56 PM
C Programming
,
Nested Structures
,
Programming
,
Singly Linked List
,
Stack
No comments
:
This is a program that stacks (push) values to a certain range indicated by the user.
Will include an image of the visualization soon, as well as code comments... (updated)
Program code:
If you have any question, place a comment below.
Will include an image of the visualization soon, as well as code comments... (updated)
Program code:
#include<stdio.h>
struct stack
{
int data;
struct stack *next;
};
struct range
{
int rangel, rangeh;
struct range *next;
struct stack *up;
}*range_start=NULL;
void display(int limit)
{
struct range *current;
int i,j,x=1,y=limit+2,ry=limit+2,ly=0;
current=range_start;
while(current!=NULL)
{
if(x>=80)
{
ly=y+1;
y=y+((limit+2)+1);
x=1;
ry=y;
}
if(ly+limit>=24)
{
gotoxy(1,25);
printf("press any key to continue...");
getch();
clrscr();
x=1;
y=limit+2;
ry=limit+2;
ly=0;
}
if(x==1)
{
for(i=1+ly;i<=y;i++)
{
gotoxy(1,i);
printf("|");
}
}
gotoxy(x+1,y);
if(current->rangel<10&¤t->rangeh>9)
{
printf(" 0%d-%d",current->rangel,current->rangeh);
}
else if(current->rangeh<10)
{
printf(" 0%d-0%d",current->rangel,current->rangeh);
}
else
{
printf(" %d-%d",current->rangel,current->rangeh);
}
x=x+4;
for(j=x,i=1;i<8;i++,j++)
{
gotoxy(j-3,y-1);
printf("-");
}
y=y-1;
while(current->up!=NULL)
{
y=y-1;
gotoxy(x,y);
printf("%d",current->up->data);
current->up=current->up->next;
}
x=x+4;
y=ry;
current=current->next;
}
}
void insertRange(int rangel, int rangeh)
{
struct range *new_node,*current;
if(range_start==NULL)
{
new_node=(struct range *)malloc(sizeof(struct range));
new_node->rangel=rangel;
new_node->rangeh=rangeh;
new_node->up=NULL;
new_node->next=NULL;
range_start=new_node;
current=new_node;
}
else
{
current=range_start;
while(current->next!=NULL)
{
current=current->next;
}
new_node=(struct range *)malloc(sizeof(struct range));
new_node->rangel=rangel;
new_node->rangeh=rangeh;
new_node->up=NULL;
new_node->next=NULL;
current->next=new_node;
current=new_node;
}
}
void insertStackData(int data)
{
struct range *current;
struct stack *new_node,*c;
current=range_start;
/*find range*/
while(current!=NULL)
{
if(data>=current->rangel&&data<=current->rangeh)
{
/*insert data to stack*/
if(current->up==NULL)
{
new_node=(struct stack *)malloc(sizeof(struct stack));
new_node->data=data;
new_node->next=NULL;
current->up=new_node;
break;
}
else
{
c=current->up;
while(c->next!=NULL)
{
c=c->next;
}
new_node=(struct stack *)malloc(sizeof(struct stack));
new_node->data=data;
new_node->next=NULL;
c->next=new_node;
break;
}
}
current=current->next;
}
}
void stack(int limit,int size)
{
int i=0,rangel=0,rangeh=size-1;
int data;
clrscr();
/*inserting to node*/
while(rangel<100)
{
if(rangeh>99)
{
rangeh=99;
}
insertRange(rangel,rangeh);
rangel=rangeh+1;
rangeh=rangeh+size;
}
clrscr();
while(i<limit)
{
printf("Enter value %d: ",i+1);
scanf("%d",&data);
if(data>=0&&data<=99)
{
insertStackData(data);
i++;
}
else
{
printf("Invalid input! Enter a value from 0-99\n");
}
}
clrscr();
display(limit);
}
void freeAllNodes()
{
free(range_start);
}
int getLimit()
{
int limit;
while(1)
{
printf("Enter number of inputs: ");
scanf("%d",&limit);
if(limit<0)
{
printf(" -Size cannot be lesser than zero!\n");
}
else
{
break;
}
}
return limit;
}
int getSize()
{
int size;
while(1)
{
printf("Enter size/range: ");
scanf("%d",&size);
if(size<1)
{
printf(" -Size cannot be equal to/lesser than 0!\n");
}
else if(size>99)
{
printf(" -Size cannot be equal to/greater than 100!\n");
}
else
{
break;
}
}
return size;
}
main()
{
int limit,size;
char choice=NULL;
clrscr();
while(1)
{
limit=getLimit();
size=getSize();
stack(limit,size);
while(choice!='Y'||choice!='y'||choice!='N'||choice!='n')
{
gotoxy(1,25);
printf("Again [y/n]? ");
choice=getche();
switch(choice)
{
case 'Y': //same with case 'y'
case 'y': /*free all nodes*/
freeAllNodes();
clrscr();
limit=getLimit();
size=getSize();
stack(limit,size);
break;
case 'N': //same with case 'n'
case 'n': //PROGRAM EXIT
exit(1);
break;
default:
gotoxy(1,25);
printf("Invalid input! press any key....");
getch();
gotoxy(14,25);
printf("\t\t\t\t");
break;
}
}
}
}
If you have any question, place a comment below.
Tuesday, February 3, 2015
DC Circuits: Calculating the Total Resistance of Parallel Resistances Problem #1
A 20 Ohms resistor, 5 Ohms resistor, and 1.5 Volts source are all connected in parallel with each other. Calculate the Total Resistance of the circuit, Voltage across both resistors, Total Current, and the current through each resistor.
Let's draw the circuit:
Calculating the Total Current IT,
Calculating voltage across each resistor - Parallel elements have the same voltage values.
Calculating Currents I1 and I2 - Parallel elements have different current values.
To check,
If you have any question, place a comment below.
Let's draw the circuit:
Solution:
I = \frac{V}{R}
Calculating the total resistance,
R_T = \frac{R_1R_2}{R_1+R_2}
R_T = \frac{(20\Omega)(5\Omega)}{20\Omega+5\Omega}
R_T = 4\Omega
Calculating the Total Current IT,
I_T = \frac{V_{source}}{R_T}
I_T = \frac{1.5V}{4\Omega}
I_T = 0.375A
Calculating voltage across each resistor - Parallel elements have the same voltage values.
Calculating Currents I1 and I2 - Parallel elements have different current values.
I_1 = \frac{V_{source}}{R_1}
I_1 = \frac{1.5V}{20\Omega}
I_1 = 0.075A
I_2 = \frac{V_{source}}{R_2}
I_2 = \frac{1.5V}{5\Omega}
I_2 = 0.3A
To check,
I_T = I_1+I_2
I_T = (0.075A)(0.3A)
I_T = 0.375A
(same as above)If you have any question, place a comment below.
Sunday, February 1, 2015
DC Circuits: Calculating Voltage Drops and Total Current Problem #1
Two resistors in series, 100 Ohms and 50 Ohms in values, are connected in series to a 5 Volts source. What is the voltage drop across each of the resistor? What is the total current I?
Firstly, we need to draw the circuit to better understand it.
Solution:
Calculate the total resistance. Learn how to calculate total resistance here.
Solving for the total current,
Solving for voltage drops across the resistors,
We use the same current value in solving both voltage drops because elements connected in series have equal currents flowing through them. The sum of all the voltage drops is equal to the voltage source.
If you have questions about this example, place a comment below.
Firstly, we need to draw the circuit to better understand it.
Solution:
I = \frac{V}{R}
Calculate the total resistance. Learn how to calculate total resistance here.
R_T = R_1+R_2
R_T = 100\Omega+50\Omega
R_T = 150\Omega
Solving for the total current,
I_T = \frac{V}{R}
I_T = \frac{5V}{150\Omega}
I_T = 0.033333333333 Amperes = 33.333333333333x10^{-3} Amps
I_T = 33.33 mA
Solving for voltage drops across the resistors,
V_{R1} = (I_T)(R_1)
V_{R1} = (33.33 mA)(100\Omega)
V_{R1} = 3.33V
V_{R2} = (I_T)(R_1)
V_{R2} = (33.33 mA)(50\Omega)
V_{R2} = 1.67V
We use the same current value in solving both voltage drops because elements connected in series have equal currents flowing through them. The sum of all the voltage drops is equal to the voltage source.
V_{source} = 3.33V+1.67V
V_{source} = 5V
If you have questions about this example, place a comment below.
Subscribe to:
Posts
(
Atom
)