Saturday, January 31, 2015
AC Circuits: Calculating the Total Impedance Problem #1
A 100-ohm resistor, 5mH inductor, and a 10uF capacitor are connected in series to a 7V (Volts), 1kHz (kiloHertz) source. Calculate the total reactance and impedance of the circuit.
See how to get the equivalent reactance here. We need the equivalent reactance in order to calculate for the total impedance.Here is how to get the total impedance, if you do not know yet.
Solution:
Z_t = R + jX_{eq}
Z_t = R + j(X_L - X_C)
Z_t = 100\Omega + j(31.42\Omega - 15.92\Omega)
Rectangular form:
Z_t = 100\Omega + j15.5\Omega
Polar form:
Z_t = 101.19\angle8.81^{\circ}\Omega
Check below for more relevant sample problems with their answers and solutions. If you have questions about the solution or answer, place a comment below.
Monday, January 26, 2015
C Programming: Inserting at Start and End of a Singly Linked List and Displaying the List
Here is a program which inserts at the start and end of a Singly Linked List, as well as, display the list from start to end.
The program consists of 4 functions:
1. insertEnd(int data): void
-This function inserts the data entered by the user at the end of the list
2. insertStart(int data): void
-This function inserts the data entered by the user at the start of the list
3. display(): void
-This function displays all the data entered by the user from start to end
4. main()
-Well, this is our main function.
Here are the codes.
You may use this or any part of this program for noncommercial use, i.e. your assignments, projects, teaching programs.
If you have questions/suggestions, quickly place a comment below.
The program consists of 4 functions:
1. insertEnd(int data): void
-This function inserts the data entered by the user at the end of the list
2. insertStart(int data): void
-This function inserts the data entered by the user at the start of the list
3. display(): void
-This function displays all the data entered by the user from start to end
4. main()
-Well, this is our main function.
Here are the codes.
struct node
{
int data; /*the data*/
struct node *next; /*This is a structure within a structure.*/
}*start=NULL,*end=NULL; /*We instantiate var start and end with NULL since there is no node yet*/
void insertEnd(int data)
{
/*new_node is the new node we create each time this function is called.
current is for keeping track of the current node we are dealing with.*/
struct node *new_node,*current;
if(end==NULL) /*if the list is empty*/
{
/*printing something to indicate that there is no node yet. This is useful for debugging.*/
printf("no nodes. creating starting node for %d...\npress any key...",data);
getch();
/*Here, we allocate memory space for the variable new_node of type node.*/
new_node=(struct node *)malloc(sizeof(struct node));
/*We store the passed value of data to the variable data inside new_node.*/
new_node->data=data;
/*We instantiate the variable next inside new_node with NULL because there is nothing next
to this current node*/
new_node->next=NULL;
/*Since this is the first and only node being created, we will store this node to the
variable start and end*/
start=new_node;
end=start;
/*new_node is the current node we are dealing with.*/
current=new_node;
}
else /*If the list is not empty, we will go through the list until the end and add a new node
there.*/
{
current=start; /*let's start from the start*/
while(1) /*an infinite loop*/
{
if(current->next!=NULL) /*if this current node is not the end of the list,*/
{
current=current->next; /*we will look at the next one*/
} /*until there is none next*/
else
{
printf("nodes exist. creating new node for %d...\npress any key...",data);
getch();
new_node=(struct node *)malloc(sizeof(struct node));
new_node->data=data;
new_node->next=NULL;
end=new_node; /*this is the last in the list, thus, we store this to var end*/
current->next=new_node; /*this is next to the current node*/
current=new_node; /*then, this will be our current node*/
break; /*we'll break the infinity loop here*/
}
}
}
printf(" done\n"); /*printing something to indicate we are done inserting*/
}
void insertStart(int data)
{
/*We don't need a current variable of type node in this function since, we don't need to
traverse through the list.*/
struct node *new_node;
if(end==NULL) /*This is just the same with the creation of the first node in the insertEnd
function above except that we don't have the variable current*/
{
printf("no nodes. creating starting node for %d...\npress any key...",data);
new_node=(struct node *)malloc(sizeof(struct node));
new_node->data=data;
new_node->next=NULL;
start=new_node;
end=start;
}
else
{
printf("nodes exist. creating a new node for %d...\npress any key...",data);
getch();
new_node=(struct node *)malloc(sizeof(struct node));
new_node->data=data;
new_node->next=start; /*since we are inserting at the start of the list, this new node will
be ahead of the starting node. In other words, start will be next
to this in the list.*/
start=new_node; /*...and the starting node will, now, be this new node we are creating*/
}
printf("done");
}
void display()
{
struct node *current; /*Here, we are only using the variable current to traverse through the
list*/
current=start; /*Let's start from the start of the list to the user*/
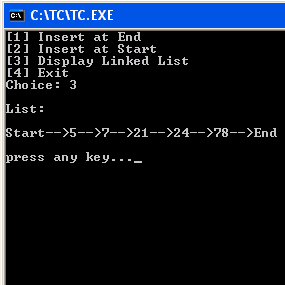
printf("\nList:\n\nStart-->"); /*indicating the start of the list*/
while(current!=NULL) /*while this current node is not the end of the list, (next to the end of
the list is NULL)*/
{
printf("%d-->",current->data); /*printing the data*/
current=current->next; /*let's go to the next node*/
}
printf("End\n\npress any key..."); /*indicating the end of the list to the user*/
getch();
}
main()
{
/*This is easy right here. If you have any question in this part, though, just place a comment
below*/
int data,pos,choice;
while(1)
{
clrscr();
printf("[1] Insert at End\n[2] Insert at Start\n[3] Display Linked List\n[4] Exit\nChoice: ");
scanf("%d",&choice);
switch(choice)
{
case 1:
clrscr();
printf("Inserting at End...\n\nEnter data: ");
scanf("%d",&data);
insertEnd(data);
break;
case 2:
clrscr();
printf("Inserting at Start...\n\nEnter data: ");
scanf("%d",&data);
insertStart(data);
break;
case 3:
display();
break;
case 4:
exit(1);
break;
default:
printf("\nPlease choose one operation from the menu.")
break;
}
}
}
You may use this or any part of this program for noncommercial use, i.e. your assignments, projects, teaching programs.
If you have questions/suggestions, quickly place a comment below.
Thursday, January 22, 2015
AC Circuits: Equivalent Reactance of a Series RLC Circuit problem #1
A 100 Ohms resistor, 5 mH inductor, and a 10 uF capacitor are connected in series to a 7V (Volts), 1kHz (kiloHertz) source. Calculate the equivalent reactance.
To calculate the equivalent reactance of the circuit in the figure below, we need to use the formulas written HERE.
Solving for the inductive reactance,
Solving for the capacitive reactance,
Note: As much as possible, don't round off the values except the final answer in order to have minimal errors. This is applicable not just with this topic but to almost any.
Now, solving for the equivalent reactance,
If you have any question, place a comment below. We will solve this circuit's impedance in another post.
Update: Solution and answer for the total impedance is here!
To calculate the equivalent reactance of the circuit in the figure below, we need to use the formulas written HERE.
Solving for the inductive reactance,
X_L = 2{\pi}f{L_1}
X_L = 2{\pi}(1 kHz)(5 mH)
X_L = 2{\pi}(1000 Hz)(5x10^{-3} H)
X_L = 31.42\Omega
Solving for the capacitive reactance,
X_C = \frac{1}{2{\pi}f{C_1}}
X_C = \frac{1}{2{\pi}(1kHz)(10{\mu}F)}
X_C = \frac{1}{2{\pi}(1000 Hz)(10x10^{-6}F)}
X_C = 15.92\Omega
Note: As much as possible, don't round off the values except the final answer in order to have minimal errors. This is applicable not just with this topic but to almost any.
Now, solving for the equivalent reactance,
X_{eq} = X_L - X_C
X_{eq} = 31.42\Omega - 15.92\Omega
X_{eq} = 15.5\Omega
If you have any question, place a comment below. We will solve this circuit's impedance in another post.
Update: Solution and answer for the total impedance is here!
Tuesday, January 20, 2015
Java Programming: Program that adds two (2) floats
Here is a program that adds two (2) floats. The program only accepts numbers. It keeps asking for input until a number is entered. The function add(float addend1, float addend2) returns the result in float.
code:
When operating on floats, the computer, sometimes, doesn't give the right answer. The computer isn't actually wrong. Read the explanation HERE. We can format the answer we print as a workaround for this (see code lines 38 to 43).
You may use this or any part of this program for noncommercial use, i.e. your assignments, projects, teaching programs.
If you have questions/suggestions, quickly place a comment below.
code:
import java.util.Scanner;
/**
*
* @author Engineering Problems and Answers (http://engineeringproblemsandanswers.blogspot.com)
*/
public class main {
public static void main(String[] args) {
float addend1, addend2, result; //declare addends and result variables
Scanner sc = new Scanner(System.in); //initialize scanner
System.out.print("Enter 1st addend: "); //ask for the 1st number
//condition keep asking until a number is entered
while (!sc.hasNextFloat()) {
System.out.print("Enter 1st addend: ");
sc.next();
}
addend1 = sc.nextFloat(); //store the number here
System.out.print("Enter 2nd addend: "); //ask for the 2nd number
//condition to keep asking until a number is entered
while (!sc.hasNextFloat()) {
System.out.print("Enter 2nd addend: ");
sc.next();
}
addend2 = sc.nextFloat(); //store the number here
result = add(addend1, addend2); /*call add method and store result to variable
result(float)*/
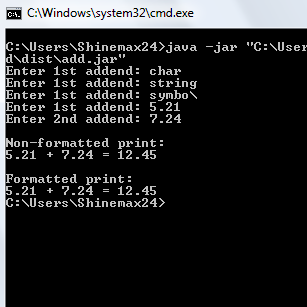
System.out.println("\nNon-formatted print:");
System.out.println(addend1+" + "+addend2+" = "+result); /*here, result value is not
accurate*/
System.out.println("\nFormatted print:");
System.out.printf("%.2f + %.2f = %.2f", addend1, addend2, result); /*format to decimal
places (result is
rounded off) in order
to get a more accurate
result value*/
}
private static float add(float addend1, float addend2) {
return addend1 + addend2; //return the sum of the two numbers
}
}
When operating on floats, the computer, sometimes, doesn't give the right answer. The computer isn't actually wrong. Read the explanation HERE. We can format the answer we print as a workaround for this (see code lines 38 to 43).
You may use this or any part of this program for noncommercial use, i.e. your assignments, projects, teaching programs.
If you have questions/suggestions, quickly place a comment below.
Monday, January 19, 2015
Logic Circuits: 4-bit K-Map (Karnaugh Map) problem #1
Simplify the following function using K-map: F(w,x,y,z) = Σ(8,10,12,13,14)
Solution:
This is a summation of minterms, therefore, 8, 10, 12, 13, and 14 are all 1's.
We can group the four 1's (the one's in Green) since there is only 1 bit difference from bits 00 to 10 (see figure). Please, review on Gray Code to understand better. And, we can group the two 1's (1's in Red). When dealing with minterms, an x is equal to 1 and an x' is equal to 0. Zero's will be listed as x' and one's as x.
Listing them, we get:
Now, we will simplify: w+w=w, x'+x'=x, y'+y=1
Then, simplify further: (w)(x)(y')(1)=wxy'
And, we get the answer:
-------------------------------------------------------------
Ask a question or comment on this solution below.
God bless!:)
Solution:
This is a summation of minterms, therefore, 8, 10, 12, 13, and 14 are all 1's.
We can group the four 1's (the one's in Green) since there is only 1 bit difference from bits 00 to 10 (see figure). Please, review on Gray Code to understand better. And, we can group the two 1's (1's in Red). When dealing with minterms, an x is equal to 1 and an x' is equal to 0. Zero's will be listed as x' and one's as x.
Listing them, we get:
F = (w + w + w + w) (x + x + x' + x') (y' + y' + y + y) (z' + z' + z' + z') + (w + w) (x + x) (y' + y') (z' + z)
Now, we will simplify: w+w=w, x'+x'=x, y'+y=1
= (w + w) (x + x') (y' + y) (z' + z') + (w) (x) (y') (1)
Then, simplify further: (w)(x)(y')(1)=wxy'
= (w) (1) (1) (z') + wxy'
And, we get the answer:
F = wz' + wxy'
or
F = w(z' + xy')
-------------------------------------------------------------
Ask a question or comment on this solution below.
God bless!:)
Logic Circuits: 3-bit K-Map (Karnaugh Map) problem #2
Simplify the following function using K-map: F(A,B,C) = Σ(0,2,3,7)
Solution:
This is a summation of minterms, therefore, 0, 2, 3, and 7 are all 1's. We can't group the 4 of them together since they don't form a square in the K-map (see figure). We can group them by pair. Notice the ones grouped in red. They can be grouped together since the difference between bits 00 and 10 is only 1 bit, and we can only group together bits that are 1 bit apart (review Gray Code, K-map is in Gray Code). When dealing with minterms, an x is equal to 1 and an x' is equal to 0. Zero's will be listed as x' and one's as x.
We need to list the variables. For the first term (red group), A has two 0's, B has one 0 and one 1, and C has two 0's. For the second term (green group), A has one 0 and one 1, B has two 1's, and C has two 1's as well.
Boolean Algebra Theorems state that x'+x'=x', x+x=x, x'+x=1
They, also, state that x∙x=x, x∙1=x, and x'∙1=x'. Thus, we get the answer.
-------------------------------------------------------------
Ask a question or comment on this solution below.
Solution:
We need to list the variables. For the first term (red group), A has two 0's, B has one 0 and one 1, and C has two 0's. For the second term (green group), A has one 0 and one 1, B has two 1's, and C has two 1's as well.
F = (A' + A') (B' + B) (C' + C') + (A' + A) (B + B) (C + C)
Boolean Algebra Theorems state that x'+x'=x', x+x=x, x'+x=1
= (A' ∙ 1 ∙ C') + 1 ∙ B ∙ C
F = (A' ∙ C) + (B ∙ C)
-------------------------------------------------------------
Ask a question or comment on this solution below.
Saturday, January 17, 2015
Logic Circuits: 3-bit K-map (Karnaugh Map) problem #1
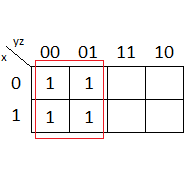
Simplify the following function using K-map: F(x,y,z) = Σ(0,1,4,5)
Solution:
This is a summation of minterms, therefore, 0, 1, 4, and 5 are all 1's. We can group the 4 of them since they form a square in the K-map (see figure). When dealing with minterms, an x is equal to 1 and an x' is equal to 0. Zero's will be listed as x' and one's as x.
Now, we need to list the variables. x has two 0's and two 1's. y has four 0's. And, z has two 0's and two 1's.
We need to simplify. Boolean Algebra Theorems state that x'+x'=x', and x'+x=1
It, also, states that x∙1=x. Thus, we get the answer
-------------------------------------------------------------
Ask a question or comment on this solution below.
Solution:
Now, we need to list the variables. x has two 0's and two 1's. y has four 0's. And, z has two 0's and two 1's.
F = (x'+x'+x+x) (y'+y'+y'+y') (z'+z'+z+z)
We need to simplify. Boolean Algebra Theorems state that x'+x'=x', and x'+x=1
= (x'+x) (y'+y') (z'+z)
= 1 ∙ y' ∙ 1
It, also, states that x∙1=x. Thus, we get the answer
-------------------------------------------------------------
Ask a question or comment on this solution below.
Subscribe to:
Posts
(
Atom
)